四边形的内角和等于多少度
的有关信息介绍如下:360度。
凸四边形的内角和和外角和均为360度。多边形的内角和计算公式:〔n-2〕×180°(n为边数)。
多边形内角和定理证明:
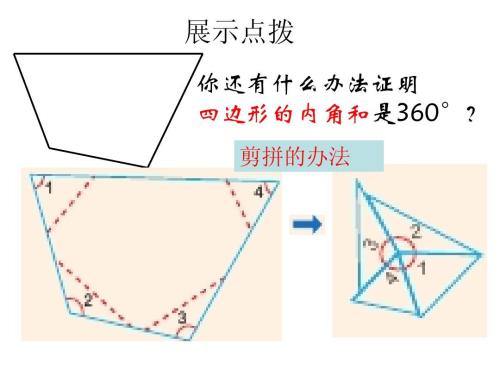
证法:在n边形内任取一点O,连结O与各个顶点,把n边形分成n个三角形.
因为这n个三角形的内角的和等于n·180°,以O为公共顶点的n个角的和是360°
所以n边形的内角和是n·180°-2×180°=(n-2)·180°(n为边数)
即n边形的内角和等于(n-2)×180°(n为边数)
扩展资料
分类:
1、凸四边形
四个顶点在同一平面内,对边不相交且作出一边所在直线,其余各边均在其同侧。平行四边形(包括:普通平行四边形,矩形,菱形,正方形)。梯形(包括:普通梯形,直角梯形,等腰梯形)。
2、凹四边形
凹四边形四个顶点在同一平面内,对边不相交且作出一边所在直线,其余各边有些在其异侧。
依次连接四边形各边中点所得的四边形称为中点四边形。不管原四边形的形状怎样改变,中点四边形的形状始终是平行四边形。
中点四边形的形状取决于原四边形的对角线。若原四边形的对角线垂直,则中点四边形为矩形;若原四边形的对角线相等,则中点四边形为菱形;若原四边形的对角线既垂直又相等,则中点四边形为正方形。
参考资料来源:百度百科-多边形内角和定理
参考资料来源:百度百科-四边形