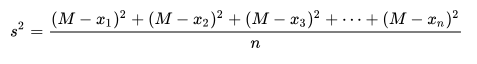指数分布的期望和方差怎么求?

指数分布的期望和方差怎么求?

如下：

指数分布的参数为λ，则指数分布的期望为1/λ；方差为（1/λ）^2。

E(X)==∫x*f(x)dx==∫λx*e^(-λx)dx=-(xe^(-λx)+1/λ*e^(-λx))|(正无穷到0)=1/λ。

E(X^2)==∫x^2*f(x)dx=∫x^2*λ*e^(λx)dx=-(2/λ^2*e^(-λx)+2x*e^(-λx)+λx^2*e^(-λx))|(正无穷到0)=2/λ^2。

DX=E(X^2)-(EX)^2=2/λ^2-(1/λ)^2=1/λ^2。

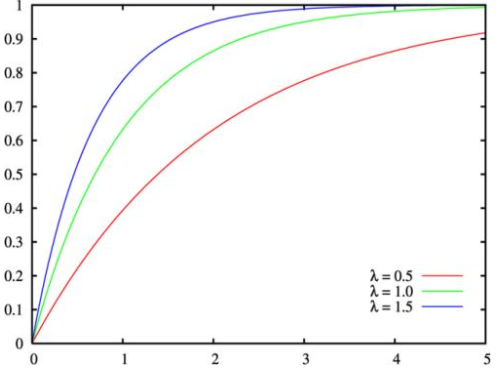
在概率理论和统计学中，指数分布（也称为负指数分布）是描述泊松过程中的事件之间的时间的概率分布，即事件以恒定平均速率连续且独立地发生的过程。 这是伽马分布的一个特殊情况。 它是几何分布的连续模拟，它具有无记忆的关键性质。 除了用于分析泊松过程外，还可以在其他各种环境中找到。

指数分布与分布指数族的分类不同，后者是包含指数分布作为其成员之一的大类概率分布，也包括正态分布，二项分布，伽马分布，泊松分布等等。

指数函数的一个重要特征是无记忆性（Memoryless Property，又称遗失记忆性）。这表示如果一个随机变量呈指数分布，当s,t>0时有P(T>t+s|T>t)=P(T>s)。即，如果T是某一元件的寿命，已知元件使用了t小时，它总共使用至少s+t小时的条件概率，与从开始使用时算起它使用至少s小时的概率相等。