奇函数的特点
的有关信息介绍如下:1、奇函数图象关于原点(0,0)对称。
2、奇函数的定义域必须关于原点(0,0)对称,否则不能成为奇函数。
3、若f(x)为奇函数,且在x=0处有意义,则f(0)=0
4、设f(x)在定义域I上可导,若f(x)在I上为奇函数,则f(x)的导函数在I上为偶函数。
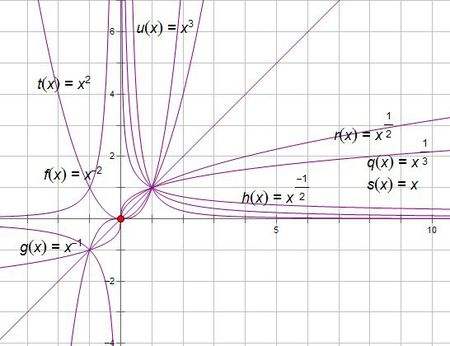
扩展资料:
奇函数的发展:
1、欧拉最早定义
若用-x代替x,函数保持不变,则称这样的函数为偶函数(拉丁文functionespares)。欧拉列举了三类偶函数和三类奇函数,并讨论了奇偶函数的性质。
2、欧拉拓展概念
1748年,欧拉出版他的数学名著《无穷分析引论》,将函数确立为分析学的最基本的研究对象。在第一章,他给出了函数的定义、对函数进行了分类,并再次讨论了两类特殊的函数:偶函数和奇函数。
3、后世发展演变
虽然达朗贝尔在《 大百科全书》 中给出了函数的定义,并介绍了有理函数、无理函数、齐次函数、相似函数,但只字未提“奇函数”和“偶函数”这两种特殊函数。
奇、偶函数概念以及华里司所引入的新名词在19世纪上半叶的英语世界里尚未得到广泛传播和普遍关注.相应地,两个概念也就不见于中国晚清的西方数学译著。直到20世纪初,两个概念才传入中国。1938年出版的《算学名词汇编》
和1945年出版的《数学名词》 中都收录了两个名词。
参考资料来源:百度百科—奇函数



