不动点法解数列通项公式问题
的有关信息介绍如下:当f(x)=x时,x的取值称为不动点,不动点是我们在竞赛中解决递推式的基本方法。
典型例子: a(n+1)=(a(an)+b)/(c(an)+d)
注:我感觉一般非用不动点不可的也就这个了,所以记住它的解法就足够了。 我们如果用一般方法解决此题也不是不可以,只是又要待定系数,又要求倒数之类的,太复杂,如果用不动点的方法,此题就很容易了。
令x=(ax+b)/(cx+d) ,即 ,cx2+(d-a)x-b=0 。令此方程的两个根为x1,x2, 若x1=x2 ,则有1/(a(n+1)-x1)=1/(an-x1)+p ,其中P可以用待定系数法求解,然后再利用等差数列通项公式求解。
注:如果有能力,可以将p的表达式记住,p=2c/(a+d) 若x1≠x2则有(a(n+1)-x1)/(a(n+1)-x2)=q((an-x1)/(an-x2)
其中q可以用待定系数法求解,然后再利用等比数列通项公式求解。
扩展资料:
设含有n个未知数与n个方程的非线性方程组为F(x)=0,然后把方程组改为便于迭代的等价形式x=ψ(x),由此就可以构造出不动点迭代法的迭代公式为xk+1=ψ(xk),如果得到的序列{xk}满足lim(k→∞)xk=x*,则x*就是ψ的不动点,这样就可以求出非线性方程组的解。
不动点法(fixed point method)是解方程的一种一般方法,对研究方程解的存在性、唯一性和具体计算有重要的理论与实用价值。数学中的各种方程,诸如代数方程、微分方程和积分方程等等,均可改写成 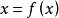 的形式,其中
的形式,其中  是某个适当的空间
是某个适当的空间 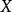 中的点,
中的点, 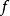 是从
是从 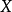 到
到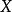 的一个映射,把点
的一个映射,把点  变成点
变成点 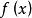 。
。
于是,方程的解就相当于映射 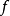 在空间
在空间 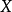 中的不动点。这一方法把解方程转化为求某个映射的不动点,故而得此名。其优点在于可以把几何、拓扑和泛函分析中较深刻的工具应用于方程论。
中的不动点。这一方法把解方程转化为求某个映射的不动点,故而得此名。其优点在于可以把几何、拓扑和泛函分析中较深刻的工具应用于方程论。
参考资料:百科百科-不动点法



