神仙道太初神兵多少锁

神仙道太初神兵多少锁

神兵并不是一笔画问题，并不是要求尽量少重复的走完某些路线，而是要走过所有的点。

另外牵涉到买锁，这就不单单是只求过所有点的最短路线的问题了。

注：以下讨论均不考虑器魂（道源）的价值，对于不急于求成的道友，算器魂的成本意义不大。

道友们一般完成神兵的步骤是，寻找格子重复最少的路线，全锁走完。

想得多一点的道友，就会再看看是不是有等价的路线，可以在某个分叉口省1,2把锁。

想得更深一点的道友，还会想哪一种最短路线需要的锁的数量最少，是全锁走锁最少的路线还是在路口随机剩下1把锁。

实际上这就是一个数学问题（个人觉得是图论领域内的，但是我不懂图论）。

下面探讨几个问题：

1）一条确定的全锁路线需要的锁数怎么算

一条确定的路线有以下3个部分组成：全图点集合、重复点、终点。

全图点集合：神兵图上全部点的集合，每个点算一次，后面简称全图。

一条完整的路线，会经过每个点，因此路线其中必然包含一个全图点集合。

重复点：不得已必须回头重复的格子。

重复点也是一条完整的路线除开全图外，剩下的部分。

终点

之所以把终点拿出来说，是因为终点的时候不需要锁了。

然后再定义一个不难理解的概念——格锁数（简称格锁）

格锁=处在某个格子时必定往下一个位置走时所需要锁的数量=相邻格子的总数量-1

由定义可以看出，每个格子有唯一且确定的格锁。

在每一条确定路线上，一个点移动到下一个点所需要的锁的数量为前一个点的格锁。

整条路线由全图点集合和重复点组成。

路线走到终点时完结。

考虑到以上3点，可以给出一条确定路线需要的总锁数的公式：

总锁数=全图格锁+重复点格锁-终点格锁

根据这个公式，对于同时存在的几条最短路线来说：

全图格锁是一定的；重复点周边格子越少，总锁数越少；终点周边格子越多，总锁数越少。

在道友不想细算的时候，可以就根据以上规律判断，耗锁最少的路线。

2）存在两条最短路线时，分叉口是留2个方向还是1个方向

这个问题可能很多道友都选择留2个方向，省一把锁。

但是，实际上应该考虑每条路线的锁耗情况。

下面还是举例说明吧。

道友们看看附件的第一张图，很简单，但是也很容易说明问题。

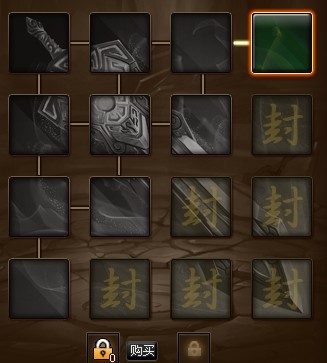
后面给出4条最短路线，见图2 图3 图4 图5，都是只重复1格的路线。

按照之前的格锁公式，4个路线需要的总锁分别是14,15,15,17，道友可以验算下，看我算错没。

而这4条路线是由两个分叉路口的不同选择形成的，这个道友们应该很容易明白。

回到我们要讨论的问题，在分叉的地方要不要省锁，让系统随机2选1呢。

分情况讨论

1)如果2个分叉口都不随机，肯定是挑14锁的那一条路线走完最优；

2)如果2个分叉口都随机，可以省下2把锁，产生4种路线的锁数分别为:12,13,13,15，出现权重各25%,期望值13.5

3)如果只在第一个分叉口（图中红点处）不随机，优选形成路线1，路线2的方向。第二个分叉口随机，可以省下1把锁，产生2种等权重的结果,13,14.期望值13.5

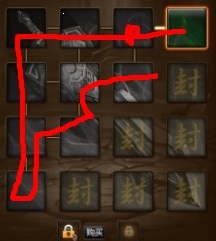
4)如果只在第一个分叉口（图中红点处）随机，第二个分叉口人为优选，最后形成路线1和路线3，省下1把锁，产生2种等权重的结果,13,14.期望值13.5。

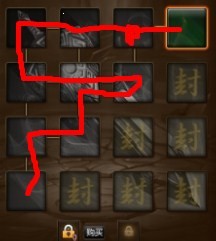
从上面4种情况的讨论看来，2,3,4的策略是优于1的。

但是，这并不意味着有等价分叉路的时候，就该随机省锁。

举个返利，两条等价路线的锁分别是16和19，随机的期望是16.5，高于16，随机并不合适。

所以说，具体情况具体分析，我只是把分析实例的方法过程列出来了，以供参考。

3）是不是最短路线的锁数是最少的

答案：不是。

直觉上，应该是重复少的路线锁耗少，但是我们再来看看公式

锁数=全图格锁+重复格锁-终点格锁

存在一些特例，某一条路线和最短路线比，多重复了一格，但是终点格锁要少很多。

比如最后那一幅图和前面4附图的路线比多重复了一格，但是总锁数，我们来算下，14+2+2-3=15，也要比图4的耗锁要少，和图2,3相当。所以，最短路线的锁耗有优劣，并不是最短路线的耗费锁数就一定比非最短路线要少

特例

不过目前看来，几种最短路线中最优的那一条的锁耗还是最少，但是我相信在某些复杂的图中是存在例外的。