函数定义域的求法

函数定义域的求法

函数的定义域一般有三种定义方法：

（1）自然定义域，若函数的对应关系有解析表达式来表示，则使解析式有意义的自变量的取值范围称为自然定义域。例如函数

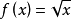
要使函数解析式有意义，则

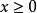
因此函数的自然定义域为

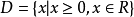
（2）函数有具体应用的实际背景。例如，函数v=f(t)表示速度与时间的关系，为使物理问题有意义，则时间

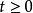
因此函数的定义域为

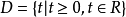
（3）人为定义的定义域。例如，在研究某个函数时，我们只关心函数的自变量x在[0,10]范围内的一段函数关系，因此定义函数的定义域为[0,10]。

扩展资料

求函数定义域的主要依据是：

(1)分式的分母不为零;

(2)偶次方根的被开方数大于等于零;

(3)对数的真数大于零;

(4)指数式、对数式的底数必须大于零且不等于1;

(5)实际问题中注意自变量的范围，比如大于0或者只能取整数等等。

参考资料来源：百度百科-定义域