平行向量公式

平行向量公式

公式如下：

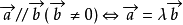
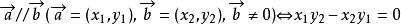
“向量共线”和“向量平行”是同一个概念。假定与某一直线共线（平行）的所有向量组成一个集合A.正是由于规定了零向量与任何向量都平行，才有0∈A，于是这个集合A中的向量才满足下面三条：

1、任给a，b∈A,总有a+b∈A；

2、任给a，c∈A，则必存在b∈A,使a+b=c成立.我们说b=c-a;(只有封闭的运算才有逆运算）。

3、任给a，b∈A,(a≠0)，则必存在惟一的实数λ,使b=λa;反之，若a∈A,λ∈R,b=λa,则b∈A。

分别说明对于集合A，加法，减法，数乘这三种运算的结果仍然在集合A当中.我们把这分别称做加法、减法和数乘，这三种运算对于集合A是“封闭的”。

如果我们不作“零向量与任何向量都平行”的规定，那么，对于某个共线向量集合A，这有可能0A.我们给定a∈A.当然-a∈A,然而a+（-a）A。这样，加法运算对于集合A就不封闭了.类似地，向量的减法、数乘，这两种运算的封闭性也都不成立了。 

扩展资料

1、共线向量与平行向量关系

由于任何一组平行向量都可移到同一直线上，故平行向量也叫做共线向量。

2、平行向量与相等向量的关系

相等的向量一定平行，但是平行的向量并不一定相等。两个向量相等并不一定这两个向量一定要重合。只用这两个向量长度相等且方向相同即可。其中“方向相同”就包含着向量平行的含义。 

参考资料来源：百度百科-平行向量