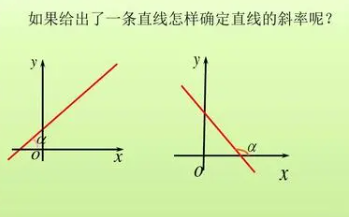
Simone两条直线垂直斜率的关系
的有关信息介绍如下：如果两条直线的斜率都存在。则，它们的斜率之积＝-1。
如果其中一条直线的斜率不存在。则，另一条直线的斜率＝0。
如果直线与x轴垂直，直角的正切值无穷大，故此直线不存在斜率。 当直线L的斜率存在时，对于一次函数y=kx+b（斜截式），k即该函数图像(直线)的斜率。
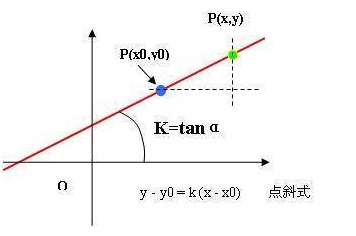
对于任意函数上任意一点，其斜率等于其切线与x轴正方向的夹角，即tanα：
斜率计算：ax+by+c=0中，k=－a/b。
直线斜率公式:k=(y2-y1)/(x2-x1)。
两条垂直相交直线的斜率相乘积为-1：k1*k2=-1。
当k>0时，直线与x轴夹角越大，斜率越大；当k<0时，直线与x轴夹角越小，斜率越小。
