ln的定义域

ln的定义域

ln的定义域是x>0，或者表达为（0，+∞）。

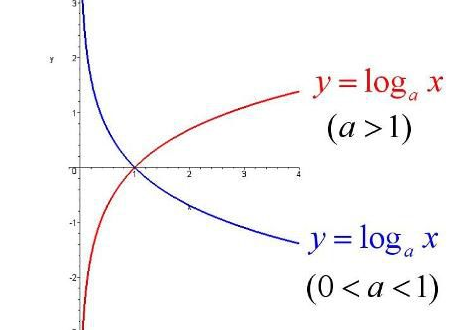
自然对数是以常数e为底数的对数，记作lnN（N>0）。根据可导必连续的性质，lnx在(0,+∞)上处处连续、可导。其导数为1/x>0，所以在（0，+∞）单调增加。又根据反常积分分别发散可知，函数的定义域为（0，+∞），以e为底，值域为R。

扩展资料：

e在科学技术中用得非常多，一般不使用以10为底数的对数。以e为底数，许多式子都能得到简化，用它是最“自然”的，所以常被叫做“自然对数”。

以前人们做乘法就用乘法，很麻烦，发明了对数这个工具后，乘法可以化成加法，即：ln（M+N） = lnM+lnN。当然后来数学家对这个数做了无数研究，发现其各种神奇之处，在对数表中出现并非偶然，而是相当自然或必然的。因此就叫它自然对数底。