面积如何定义的？

面积如何定义的？

当物体占据的空间是二维空间时，所占空间的大小叫做该物体的面积，面积可以是平面的也可以是曲面的。平方米，平方分米，平方厘米，是公认的面积单位，用字母可以表示为（m，dm，cm）。

面积是表示平面中二维图形或形状或平面层的程度的数量。表面积是三维物体的二维表面上的模拟物。面积可以理解为具有给定厚度的材料的量，面积是形成形状的模型所必需的。

面积是表示平面中二维图形或形状或平面层的程度的数量。表面积是三维物体的二维表面上的模拟物。面积可以理解为具有给定厚度的材料的量，面积是形成形状的模型所必需的，或者用单一涂层覆盖表面所需的涂料量。它是曲线长度（一维概念）或实体体积（三维概念）的二维模拟。

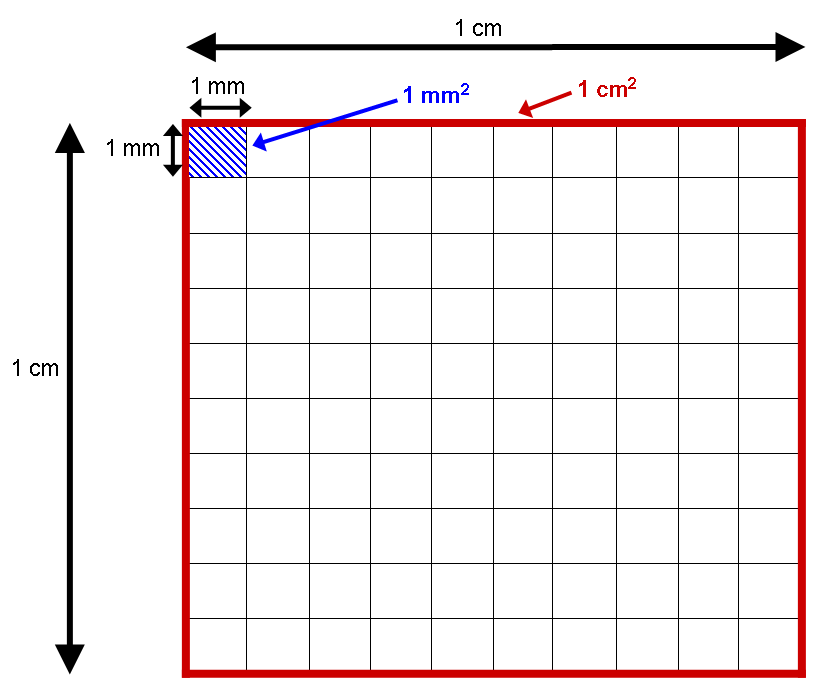
可以通过将固定尺寸的形状与正方形进行比较来测量形状的面积。在国际单位制（SI）中，标准单位面积为平方米（平方米），面积为一米长的正方形面积，面积为三平方米的形状将与三个这样的广场相同。在数学中，单位正方形被定义为具有区域1，任何其他形状或表面的面积都是无量纲实数。

有几种众所周知的简单形状的公式，如三角形，矩形和圆形。使用这些公式，可以通过将多边形分成三角形来找到任何多边形的面积。对于具有弯曲边界的形状，通常需要微积分来计算面积。事实上，确定飞机数字面积的问题是演算历史发展的主要动机。

历史

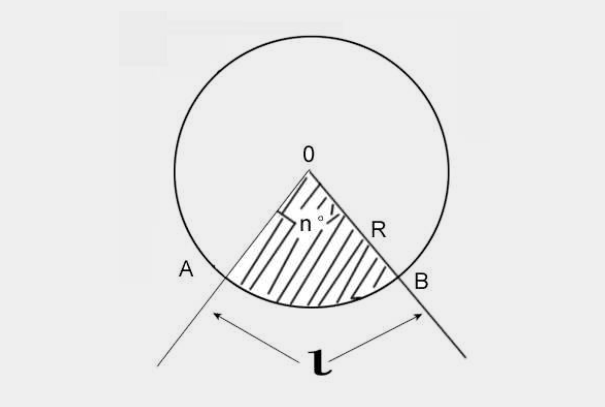
1、圆形区域

在公元前 5 世纪，希俄斯的希波克拉底首先证明了圆盘的面积（被圆圈包围的区域）与其直径的平方成正比，作为他的希波克拉底月的求积的一部分，但没有确定比例常数。同样在公元前 5 世纪，Cnidus 的 Eudoxus也发现圆盘的面积与其半径的平方成正比。

随后，欧几里得元素的第一卷处理了二维图形之间的面积相等。数学家阿基米德在他的《圆的测量》一书中用欧几里得几何的工具证明了一个圆内的面积等于一个直角三角形的面积，这个三角形的底边是圆的周长，高等于圆的半径。

（周长是 2πr，三角形的面积是底乘高的一半，得出圆盘的面积πr2。）阿基米德近似了 π 的值（因此是单位半径圆的面积） ） 和他的加倍方法，他将一个正三角形内接在一个圆上并记下它的面积，然后将边数加倍得到一个正六边形；

然后随着多边形面积越来越接近正六边形的面积，边数不断加倍圆（对外接多边形也一样）。

瑞士科学家约翰·海因里希·兰伯特( Johann Heinrich Lambert)于 1761 年证明，圆周面积与其平方半径之比π是无理数，这意味着它不等于任何两个整数的商。1794年法国数学家Adrien-Marie Legendre证明了π 2是无理数；这也证明π是无理数

1882年，德国数学家费迪南德·冯·林德曼证明了π是超越的（不是任何具有有理系数的多项式方程的解），证实了勒让德和欧拉的猜想。

2、三角区

亚历山大的 Heron（或 Hero）发现了三角形面积的Heron 公式，证明可以在他写于公元 60 年左右的书Metrica 中找到。有人认为阿基米德早在两个世纪前就知道这个公式，并且由于Metrica是古代世界可用数学知识的集合，因此该公式可能早于该工作中给出的参考文献。

在499阿耶波多，一个伟大的数学家-天文学家从古典时期的印度数学和印度天文学，表达了三角形作为一个半底座倍的高度区域Aryabhatiya（2.6）。

中国人独立于希腊人发现了一个与苍鹭公式等价的公式。它被出版了1247在鼠鼠九章（“数学伤寒九章”），以书面秦九韶。

3、四边形区域

在公元 7 世纪，Brahmagupta开发了一个公式，现在称为Brahmagupta 公式，用于计算循环四边形（内接于圆的四边形 ）的边面积。

1842 年，德国数学家卡尔·安东·布雷施奈德和卡尔·格奥尔格·克里斯蒂安·冯·施陶特独立发现了一个公式，称为布雷施奈德公式，用于计算任何四边形的面积。

以上内容参考 百度百科-面积