圆锥曲线公式

圆锥曲线公式

圆锥曲线的公式主要有以下：

1、椭圆∶焦半径∶a+ex(左焦点),a-ex(右焦点),x=a²/c

2、双曲线∶焦半径∶|a+ex|(左焦点)|a-ex|(右焦点),准线x=a²/c

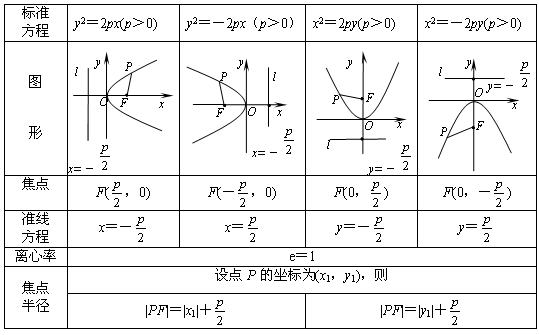
3、抛物线(y²=2px)∶焦半径∶x+p/2准线∶x=-p/2

弦长=√k²+1*√(x1+x2)²-4x1x2以上是焦点在x轴的,y轴只需将x换成y即可。

二.双曲线

1.通径长 = 2b²/a

2.焦半径公式（有8个，很难打符号的，不过可以根据极坐标方程来直接解答，比焦半径公式还快一些）

3.焦点三角形面积公式

S⊿PF1F2 =b²cot（θ/2）

三.抛物线

y²=2px （p＞0）过焦点的直线交它于A(X1,Y1),B(X2,Y2)两点

1.│AB│=X1 + X2 + p =2p/sin²θ （θ为直线AB的倾斜角）

2. Y1*Y2 = -p² ， X1*X2 = p²/4

3.1/│FA│ + 1/│FB│ = 2/p

4.结论：以AB 为直径的圆与抛物线的准线线切

5.焦半径公式： │FA│= X1 + p/2 = p/（1-cosθ）

①圆锥曲线（conic section），又称圆锥截痕、圆锥截面、二次曲线，是数学、几何学中通过平切圆锥（严格为一个正圆锥面和一个平面完整相切）得到的一些曲线。

②阿波罗尼曾把椭圆叫“亏曲线”，把双曲线叫做“超曲线”，把抛物线叫做“齐曲线”。事实上，阿波罗尼在其着作中使用纯几何方法已经取得了今天高中数学中关于圆锥曲线的全部性质和结果。

百度百科“圆锥曲线”