根号X分之一的导数
的有关信息介绍如下: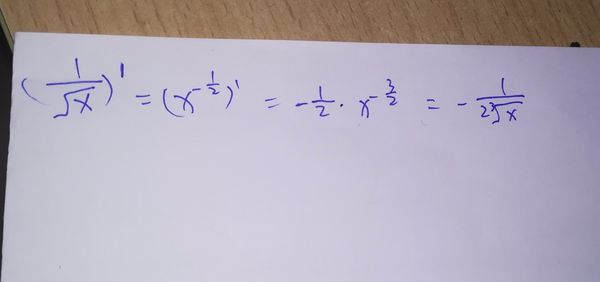
具体的解答过程如上图所示
拓展资料:
1、导数的定义
设函数y=f(x)在点x=x0及其附近有定义,当自变量x在x0处有改变量△x(△x可正可负),则函数y相应地有改变量△y=f(x0+△x)-f(x0),这两个改变量的比叫做函数y=f(x)在x0到x0+△x之间的平均变化率。
如果当△x→0时,有极限,我们就说函数y=f(x)在点x0处可导,这个极限叫做f(x)在点x0处的导数(即瞬时变化率,简称变化率),记作f′(x0)或y',即函数f(x)在点x0处的导数就是函数平均变化率。
当自变量的改变量趋向于零时的极限。如果极限不存在,我们就说函数f(x)在点x0处不可导。
常见的导数表




