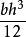周长怎么计算？

周长怎么计算？

环绕有限面积的区域边缘的长度积分，叫做周长，也就是图形一周的长度。多边形的周长的长度也相等于图形所有边的和，圆的周长=πd=2πr (d为直径，r为半径，π)，扇形的周长 = 2R+nπR÷180 (n=圆心角角度) = 2R+kR (k=弧度)。

环绕有限面积的区域边缘的长度积分，叫做周长，也就是图形一周的长度。周长用字母C表示。

周长的计算公式：

圆：C＝πd＝2πr（d为直径，r为半径，π）

三角形的周长C＝a＋b＋C（ABC是三角形的三条边）。

四边形：C＝a＋b＋C＋d（abcd是四边形的边长）。

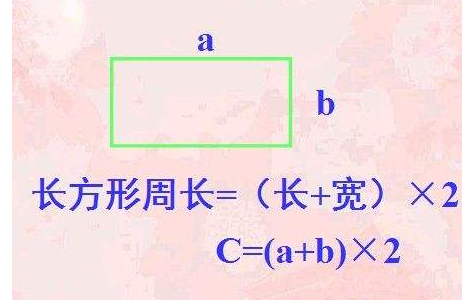
特殊：矩形：C＝2（a＋b）（a为长，b为宽）

正方形：C＝4a（a是正方形的边长）。

多边形：C＝所有边长之和。

扇形的周长：C＝2R＋nπR÷180˚（n＝圆心角）＝2R＋kR（k＝弧度）。

周长之历史上最先算出地球的周长：

古希腊的埃拉托色尼早在2000多年前就用简单的测量工具计算出了地球的周长。

埃拉托色尼发现，在距亚历山大港约800公里的塞恩市(今埃及阿斯旺附近)，夏日正午的太阳能照到井底，所以地面上直立的物体都不会有影子。

但是在亚历山大的地面上有一个非常短的影子。他认为直立物体的阴影是由太阳和亚历山大直立物体之间的夹角造成的。从两个前提，地球是一个球体和阳光以直线传播，直接从虚构的两条直线地球中心的城市塞恩和亚历山大，和两条线之间的角度应该等于亚历山大的阳光之间的角度和支柱。

如果你知道两个地方的距离在相似三角形的比例，你可以测量地球的周长。埃拉托色尼测量的角度是地球周长（360度）的50分之1的7度左右，并计算出地球的周长约为4万公里，与地球的实际周长（40万076公里）相差无几。

他还计算出太阳到地球的距离为1．47亿公里，与实际距离（1．49亿公里）惊人地接近。