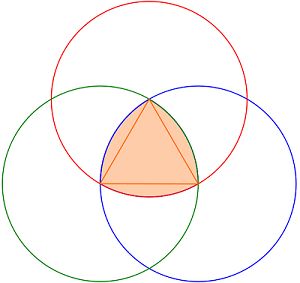
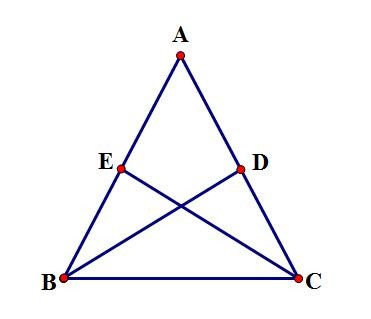
勒洛三角形的性质

勒洛三角形的性质

定宽曲线和定宽性

定宽曲线的概念：具有（类似圆的）定宽性的曲线称为定宽曲线。

定宽性，几何上的理解是：将一个圆放在两条平行线中间，使之与这两平行线相切。则可以做到：无论这个圆如何运动，它还是在这两条平行线内，并且始终与这两条平行线相切。

勒洛三角形就是典型的定宽曲线。

勒洛三角形的等宽性质很容易证明，其宽度等于构造等边三角形的边长。当勒洛三角形在边长为其宽度的正方形内旋转时，每一个角走过的轨迹基本上就是一个正方形。

面积关系

通过勒贝格积分可以算出，勒洛三角是定宽曲线所能构成的面积最小的图形，其面积为1/2[π-(3^1/2)]s^2，s为定宽宽度。

勒洛三角形的应用

在美国旧金山，有一些市政检修井井盖的形状就是勒洛三角形，其最大优点是这种形状的井盖绝不会掉到井里去。

此外，一种基于勒洛三角形的变体的设备，它能钻出方孔来，其“方度”非常之好。

勒洛不能用作轮子，因为其中心并不稳定，每旋转一圈会有三次跳动。而作为滚轴使用则是相当平稳。马自达的转子发动机也是这个原理，因为勒洛三角形是定宽曲线中面积最小的。